티스토리 뷰
농어 길이로 무게를 예측하기
03-1 k-최근접 이웃 회귀
- 회귀: 임의의 수치를 예측하는 문제
- k-최근접 이웃 회귀: k-최근접 이웃 알고리즘으로 회귀 문제를 해결. 가장 가까운 이웃의 샘플들의 평균으로 예측
- 결정계수: 회귀 문제 성능 측정 도구 0~1로 1에 가까울수록 좋다.
- 과대적합: 모델 훈련 세트 성능이 테스트 성능보다 휠씬 높을 때
- 과소적합: 테스트 세트 성능이 모두 동일하거나 테스트 세트 성능이 높을 때
데이터 준비

산점도 확인
- 길이가 길수록 몸무게 높음을 확인할 수 있다.

훈련세트와 테스트 세트 나누기

2차원 배열로 전환
- reshape() 2차원 배열로 바꾼다.

결정계수
- KNeighborsRegressor 모델에 훈련 후 결정계수 점수 확인


Mean Abolute error (평균 절대값 오차)
- 타깃 예측값 사이의 차이를 구한다.
- 예측한 모델은 평균적으로 19g의 오차가 있다.

과대적합 vs 과소적합
- train보다 test score가 높은 과소적합이 발생했다.
- 과소적합의 이유는 적절히 훈련되지 않은 경우이다.
- 현재 적은 데이터를 사용하기 때문에 과소적합이 발생했다.

과소적합 해결
- 문제를 더 복잡하게 만든다.
- 참조 이웃의 샘플 개수를 줄여서 훈련 세트의 패턴에 민감해진다.
- 이웃을 늘리면 데이터 전반에 있는 일반적인 패턴을 따른다.

기본 미션
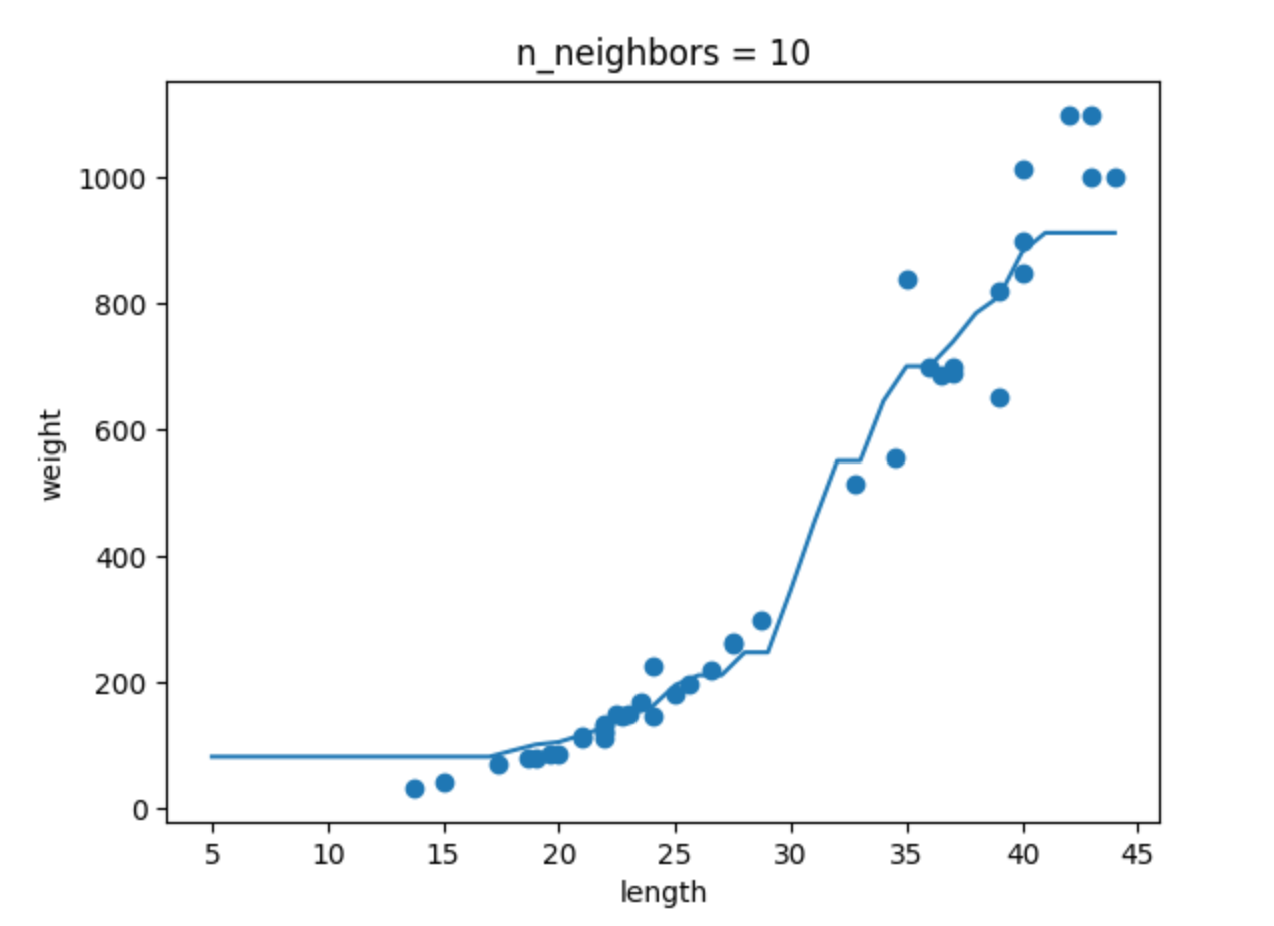
- k-최근접 이웃 회귀 모델의 k 값을 1,5,10으로 바꿔가며 훈련하기
- 농어의 길이를 5~45까지 예측 후 그래프로 나타내기
- n이 커짐에 따라 모델이 단순해지는 것을 확인

- 점은 train 데이터의 타깃값, 실선 그래프는 예측 모델


03-2 선형회귀
- 선형회귀: 특성과 타깃 사이의 관계를 가장 잘 나타내는 선형 방정식을 찾는다. 특성이 하나면 직선 방정식이 된다.
- 선형 회귀가 찾은 특성과 타깃의 관계는 계수 또는 가중치에 저장된다. 가중치는 방정식의 기울기와 절편을 의미하는 경우가 많다.
- 모델 파라미터는 선형 회귀가 찾은 머신러닝 모델이 특성에서 학습한 파라미터이다.
- 다항 회귀는 다항식을 사용하여 특성과 타깃의 관계를 나타낸다. 비선형 또는 선형 회귀로 표현할 수 있다.
앞선 데이터로 50cm 와 100cm 농어를 예측하자
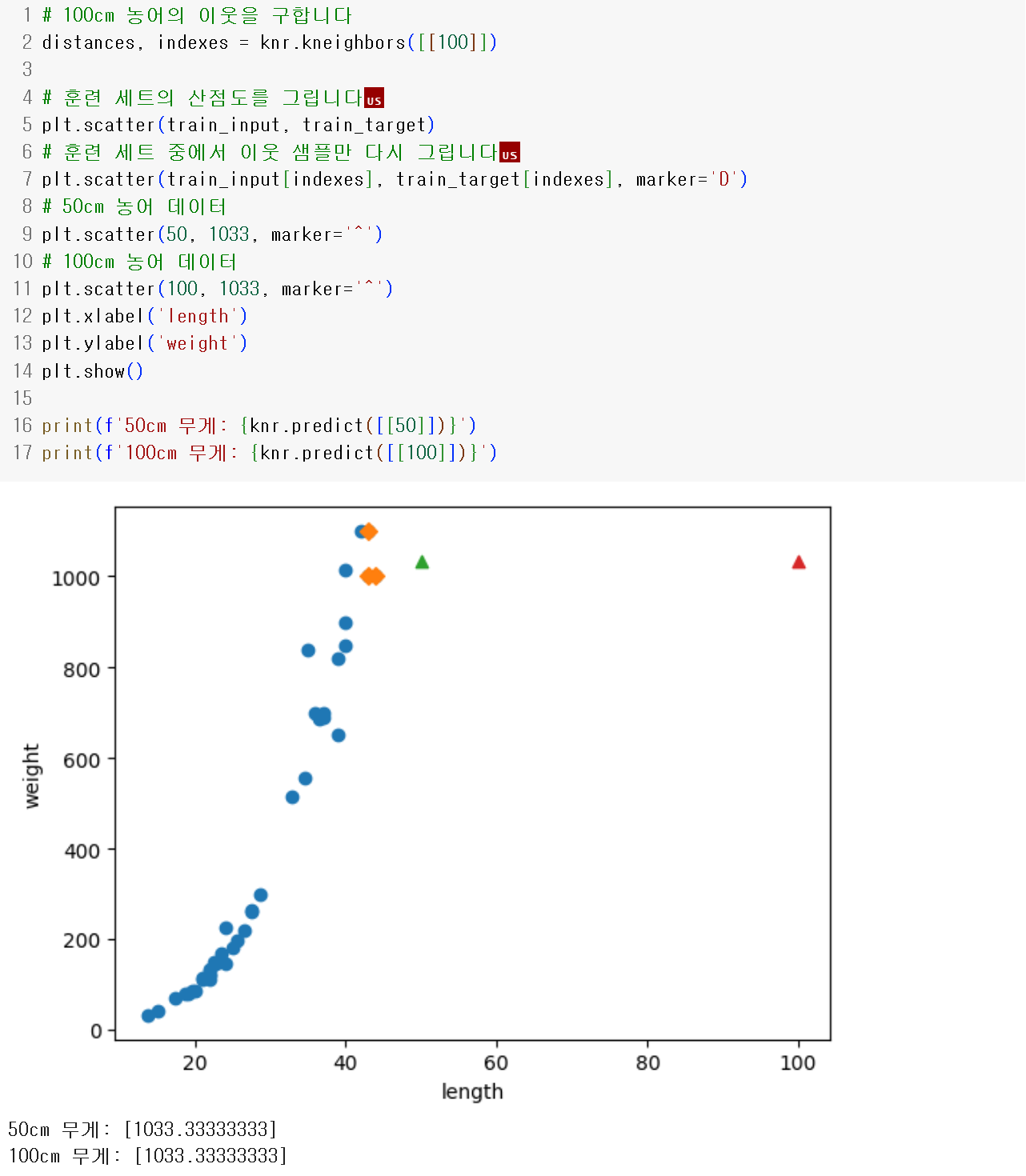
가장 가까운 샘플들의 평균을 구하기 때문에 길이가 너무 긴 농어들은 예측할 수 없어 1033.34로 예측한다.
Linear Regression
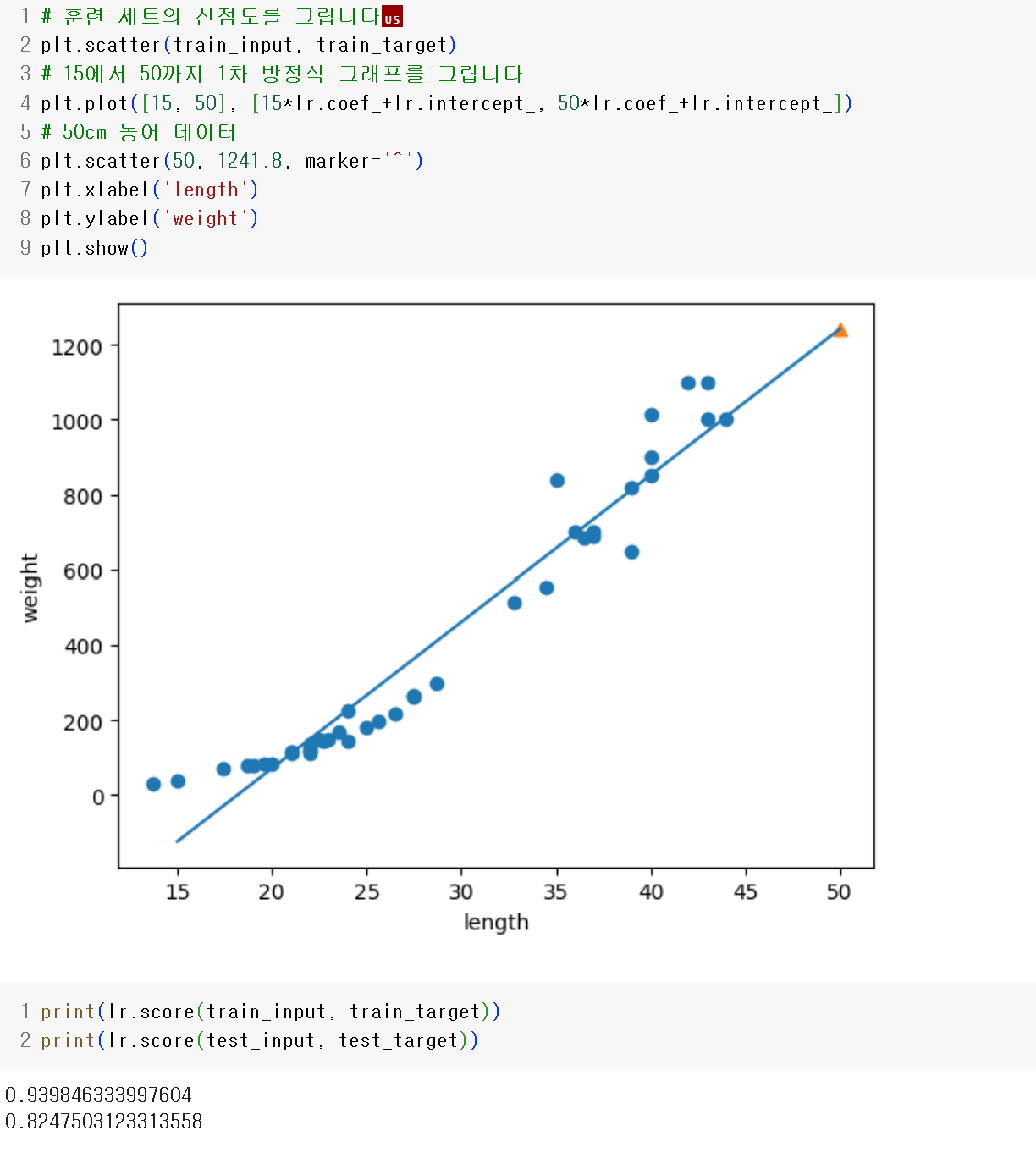
- 선형 회귀는 특성을 잘 나타낼 수 있는 직선을 찾는 것이다.
- 선형 회귀로 훈련 세트 범위 밖의 샘플을 예측할 수 있다.
$y= a * x + b$
- $x$를 농어의 길이 $y$를 농어의 무게로 바꿀 수 있다.
- 기울기 $a$는 계수(coefficient) 또는 가중치(weight)라고 부른다.
- 절편 $b$는 intercept이다.
사이킷런의 선형 회귀를 사용하면 문제를 해결할 수 있다.

- coef_ 와 intercept_를 모델 파라미터라고 부른다.
- 최적의 모델 파라미터를 찾는 것이 모델기반 학습이다.
다항 회귀
- 농어의 무게는 음수가 될 수 없다.
- 2차 방정식으로 그래프를 그려보자.
$y = a*x^2 + a*b + c$
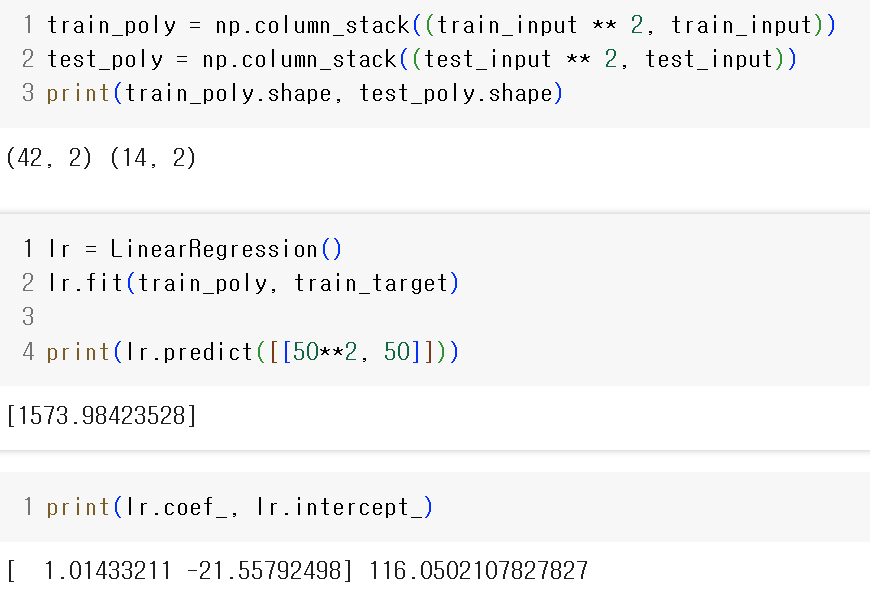
$ 무게 = 1.01 * 길이^2 -21.55 * 길이 + 116.01$


03-3 특성 공학과 규제
- 다중 회귀: 여러 개의 특성을 사용하는 회귀
- 특성 공학: 주어진 특성을 조합하여 새로운 특성을 만드는 작업
- 릿지: 규제가 있는 선형 회귀 모델 중 하나로 계수를 작게 만들어 과대적합을 완화. alpha가 클 수록 규제가 커
- 라쏘: 좌표축을 따라 최적화를 수행하는 좌표하강법을 사용. 계수 값을 릿지와 달리 0으로 만들 수 있음
데이터 준비

사이킷런 변환기
변환기(transformer)로 특성을 만들거나 전처리한다.

(42, 3) 행렬이 (42, 9)로 특성이 3개에서9개로 늘어났다.
include_bias는 절편을 추가할지 결정하는 매개변수다.
모델 학습

특성을 늘려서 비교해 본다.

특성이 너무 크기 때문에 과대적합이 발생했다.
규제
- 규제: 과도하게 학습하지 못하도록 훼방. 선형 회귀 모델의 경우 계수의 크기를 작게 만든다.
StandardScaler()로 정규화
train, test 모두 정규화

릿지 회귀

- 사전에 정의된 하이퍼 파라미터 alpha로 규제할 수 있다.
- alpha 값의 바꿔가며 결과를 그래프로 나타낸다.
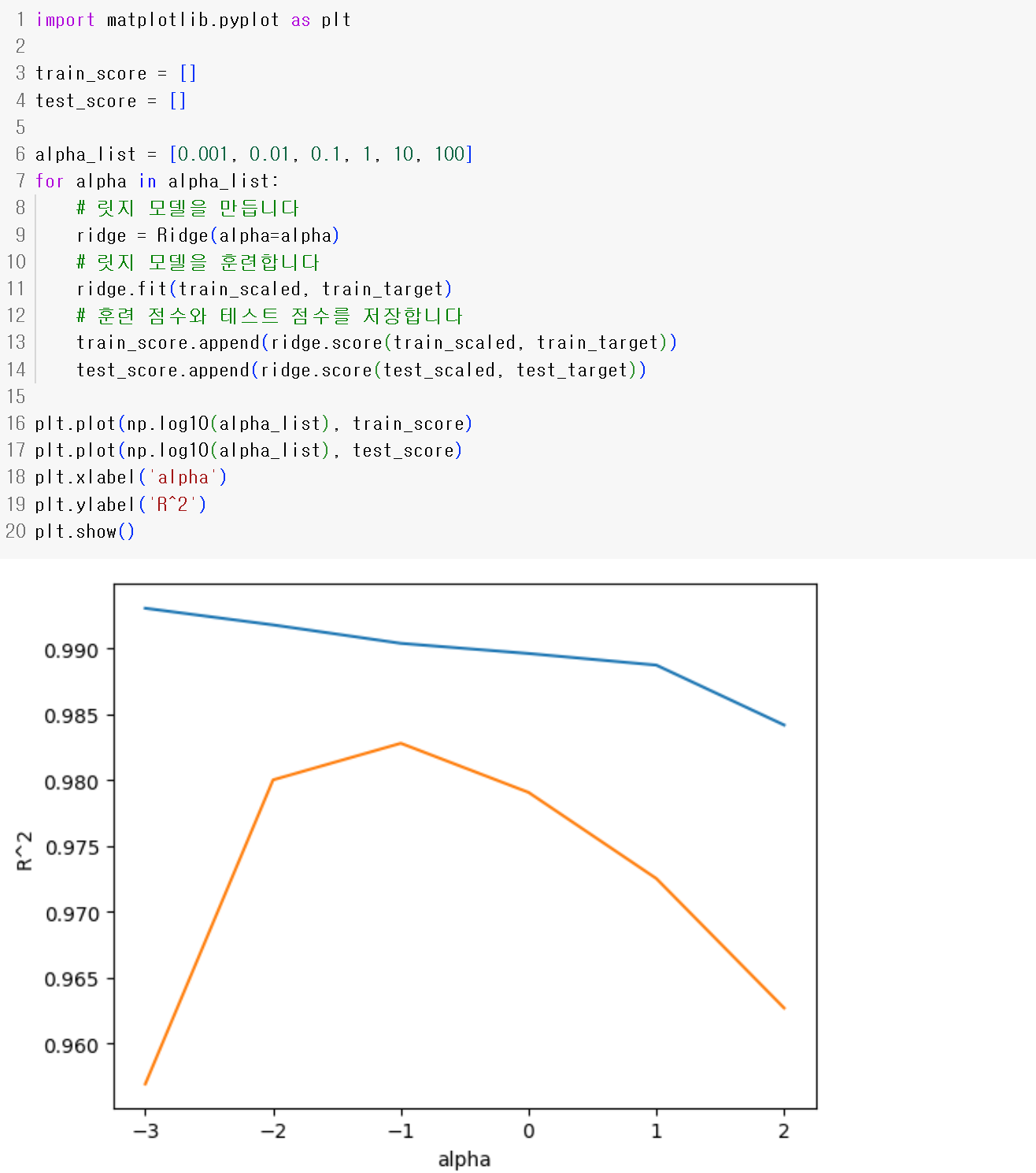
- test에서 가장 높은 -1 $10^{-1}=0.1$이 최적의 alpha이다.

라쏘



'혼공단' 카테고리의 다른 글
| [혼공족] 혼자 공부하는 머신러닝 + 딥러닝 5주차 Ch06 (0) | 2024.01.28 |
|---|---|
| [혼공족] 혼자 공부하는 머신러닝 + 딥러닝 4주차 Ch05 (0) | 2024.01.26 |
| [혼공족] 혼자 공부하는 머신러닝 + 딥러닝 3주차 Ch04 (0) | 2024.01.21 |
| [혼공족] 혼자 공부하는 머신러닝 + 딥러닝 1주차 Ch02 (1) | 2024.01.07 |
| [혼공족] 혼자 공부하는 머신러닝 + 딥러닝 1주차 Ch01 (0) | 2024.01.04 |
